지구과학에서 편서풍 파동, 서안 강화현상을 배우면서 빼놓을 수 없는 것이 바로 와도(소용돌이도, vorticity)이다. 처음 와도에 대해 배울 때는 와도가 무엇인지 감조차 잡을 수 없었다. 기상학, 해양학을 시작하고자 하는 학생들이 와도에 대해 조금 더 쉽게 이해하길 바라는 마음에서 이 글을 쓴다.
1. 와도(소용돌이도)의 정의
| 소용돌이도 또는 와도(vorticity)는 특정 지점에 위치하여 흐름을 따라 움직이는 관찰자에게 보이는 그 지점에서 연속체의 국지적 회전운동(무언가가 회전하고자 하는 경향의 척도)을 기술하는 유사벡터 장의 하나다. - 출처 : 위키백과- |
와도에 대해 위키 백과에는 위와 같이 적혀있다. 이 말만 보아서는 당최 무슨말인지 알기 어렵다. 조금 더 쉽게 이야기 하자면 물체를 회전시키려는 경향이라고 생각할 수 있다.
그렇다면 물체는 어떤 경우에 어떻게 회전하는가? 몇가지 예시를 들어 설명해보자.
2. 와도의 정성적 이해
아래의 그림과 같은 두 가지 경우를 가정해 보자. (가)는 지구가 자전할 때, 자전하는 지구 위에 있는 사람을 나타낸 것이고, (나)는 회전하는 관람차 안에 있는 사람을 나타낸 것이다. 지구와 관람차 모두 회전하고 있을 때 사람의 회전 성분에는 어떤 차이가 있을까?

(가)의 경우에는 지구가 자전하는 동안 사람도 한바퀴 돌게 된다. 아래 그림처럼 지구가 반시계방향으로 회전한다고 하자. 이때 사람의 움직임은 아래와 같다. 이와 같이 자전 성분(회전)이 존재할 때 회전류라고 부르고, 유체의 와도가 있다고 말할 수 있다.

(나)의 경우에는 관람차가 1회전 하는 동안 사람의 회전은 없다. 사람만 보았을 때는 가만히 서있는 것이다. 이렇게 자전 성분이 존재하지 않을 때 비회전류라고 부르며, 유체의 와도는 없다고 할 수 있다.

이처럼 와도는 유체 내부의 회전 성분이라고 할 수 있다. 하지만 와도는 일반적으로 입자로 이야기하지 않는다. 위에서 언급한 와도의 정의에서 볼 수 있듯이, 와도는 벡터장으로 표시한다.
이를 이해하기 위해서 이번에는 통돌이 세탁기(세워서 쓰는 세탁기) 내부의 모습을 아래와 같이 그려보았다. (가) 세탁기는 가운데 세탁봉이 돌아가면서 세탁물을 돌리는 경우이고, (나) 세탁기는 세탁기 외부의 통이 돌아가면서 세탁물을 돌리는 경우이다. 각각 통에서의 유체의 흐름은 화살표로 표시해 보았다.
각각의 통 안에서 와도가 존재하는지, 와도가 존재하지 않는지 판별하고 싶으면 막대기 하나를 통 안으로 넣어보면 된다.

(가) 세탁기의 경우 내부에서 외부로 갈 수록 유체의 속도가 느려지는 경우이다. 나무 막대를 넣으면 내부의 속도가 빠르고, 바깥의 속도가 느리기 때문에 나무 막대가 세탁봉을 중심으로 회전하기는 하지만 자전하지 않는다. 이러한 유체를 비회전류라고 한다. 유체 내부에 회전 성분이 없기 때문이다.

(나) 세탁기의 경우는 외부로 갈수록 유체의 속도가 빨라지는 경우이다. 이 때는 (가)와 다르게 나무 막대를 넣으면 막대가 세탁기와 함께 회전하게 될 것이다. 이 때 회전하려고 하는 경향 자체를 와도라고 한다. 따라서 (나) 세탁기 내부의 유체에는 와도가 존재하고, 회전류라고 부른다.

3. 와도의 정량적 표현
와도를 이제 벡터로서 표현 해보자. 와도의 방향은 전류에서의 오른손 법칙과 같다. 축을 기준으로 반시계 방향의 와도를 (+), 시계 방향의 와도를 (-)로 정의한다. 그리고 x, y, z 축에 대한 회전으로 표현 한다.
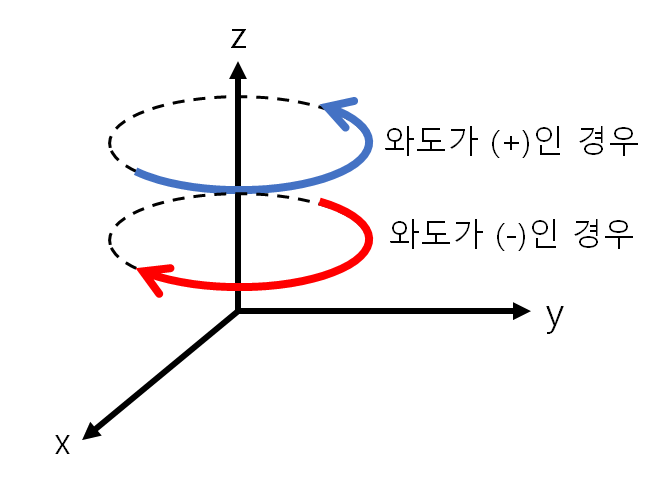
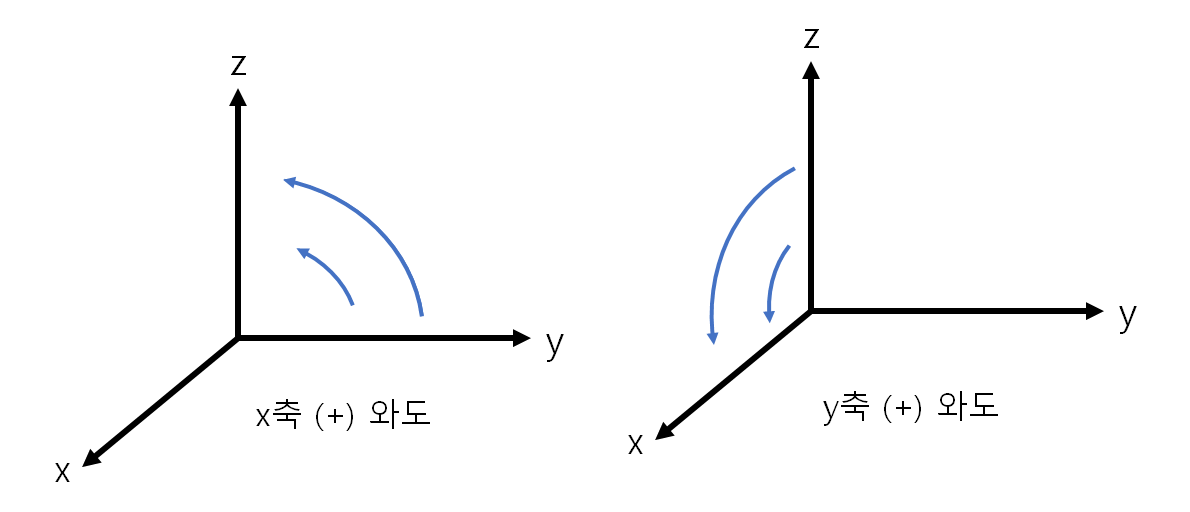
그런데 대기나 해수에서 와도를 정의 할 때, x축과 y축 방향의 와도를 고려하지 않는다. 그 이유는 와도에 의한 힘의 크기가 대기의 압력의 크기에 비해 너무나도 작기 때문이다. 이는 규모가 작은 대기 운동에서 전향력을 고려하지 않는 이유와 같다. 따라서 우리가 집중할 것은 z축에서의 와도, 즉 xy 평면에서의 와도이다.
먼저 z축에서 xy평면에서의 회전류를 아래와 같이 그려보았다. 아래 그림은 z축 방향에 대한 양의 와도(+)를 기준으로 하였다. 앞으로 x방향의 풍속을 u, y방향의 풍속을 v, z축 방향의 풍속을 w라고 표현할 것이다.
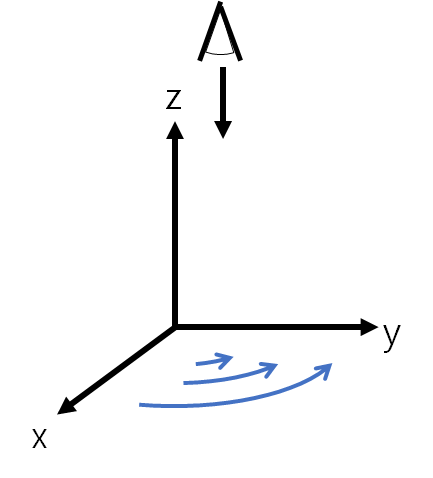
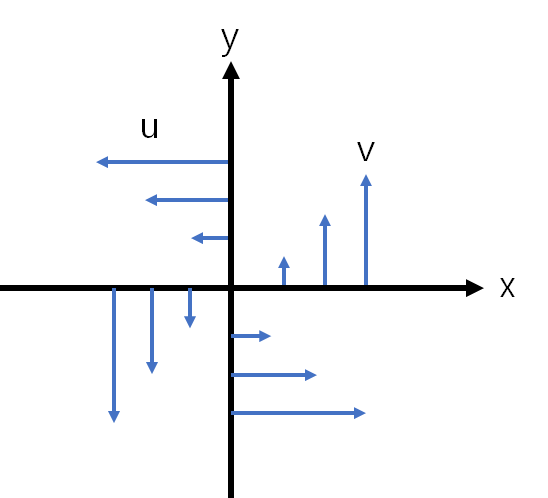
위 그림에서 x축 값이 증가할수록 y축 방향의 속도가 증가하며, y축 값이 증가할 수록 x축 방향의 속도가 (-)방향으로 증가한다. 두 값을 더하게 되면 이것이 바로 와도(ζ, zeta)이다.
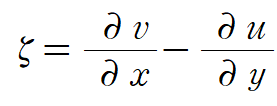
좀 더 정확하게 말하면 풍속(ω, omega)에 대한 모든 축 방향의 회전(curl)로서 표현한다.
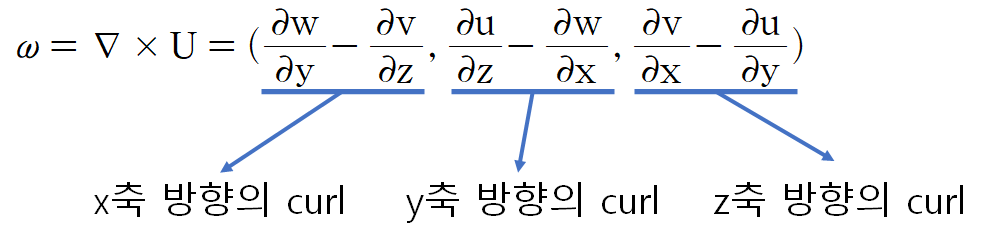
여기서 규모가 큰 기상학, 해양학에서는 연직성분 z에 대한 curl만을 고려하며, 이것을 와도(소용돌이도)라고 부른다.
4. 와도의 보존 : 상대 와도와 행성와도
앞선 글까지 이해 했다면, 이번에는 와도에 대해 더 깊이 논할 차례이다.
먼저 학생들이 배우는 와도에는 절대와도, 상대와도, 행성와도 세 가지가 있다. 절대와도는 상대와도와 행성와도의 합이며 모든 에너지가 보존 되듯이 절대 와도는 보존된다. 상대 와도는 지구 상에서 움직이는 유체가 가지는 와도이고 행성 와도는 지구의 회전에 의한 와도이다.
기체 자체의 와도인 상대 와도는 쉽게 이해할 수 있으나, 행성 와도가 무슨 말인지는 이해하기 쉽지 않다.
아래의 그림 (가)는 북쪽에서 내려본 지구의 모습과 회전 속도를 나타낸 것이고, (나)에 에 적도지방에서 극지방으로 이동하는 어떤 공기 덩어리의 위치와 좌표계를 나타낸 것이다.
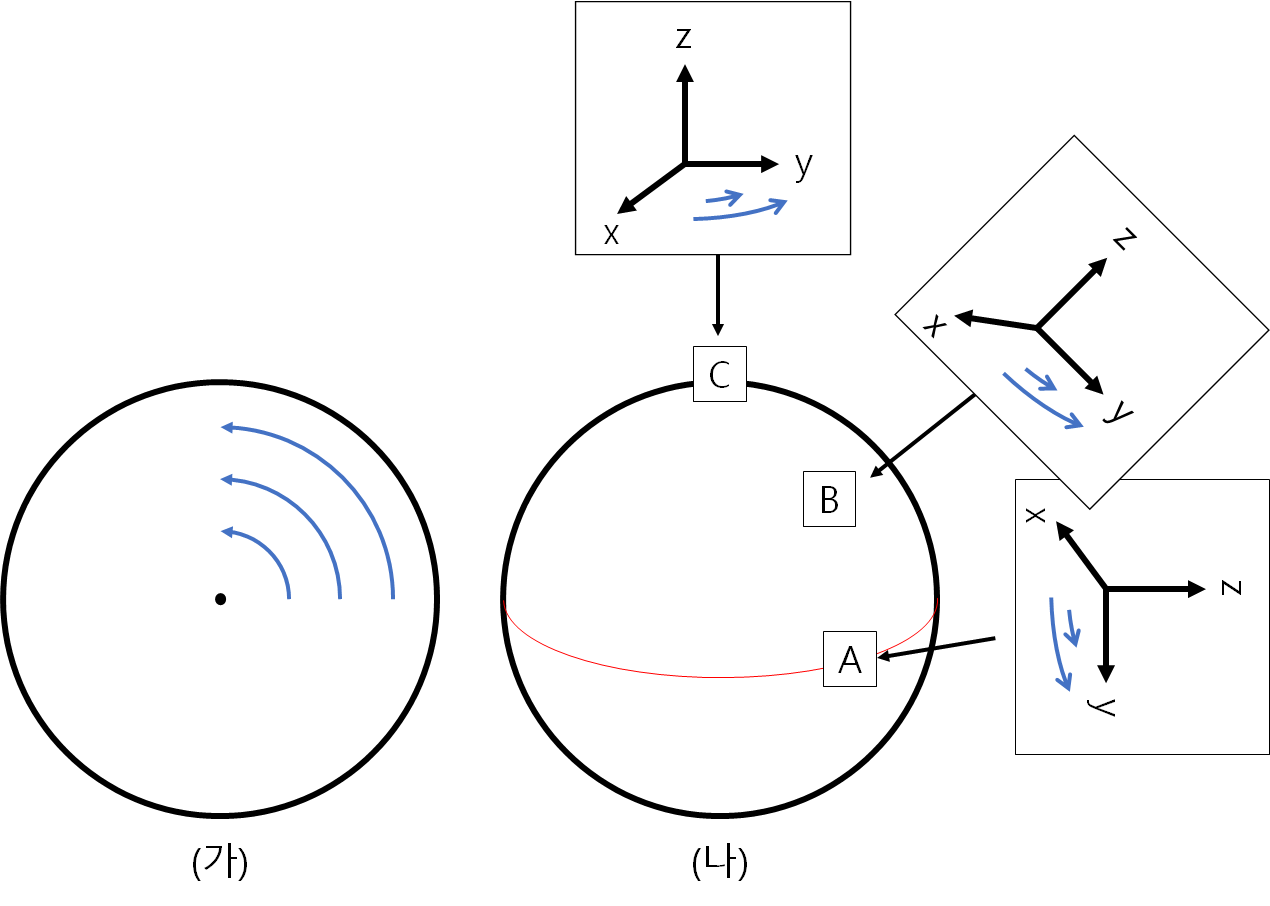
(가)에서 보았을 때 지구는 자전축을 중심으로 원판 회전을 하고 있다. 적도 부근의 회전 속도는 빠르고 극지방 부근의 회전 속도는 느리며, 지구상의 유체는 자전축 방향의 와도를 가지고 있다.
(나)에서는 어떤 공기가 적도지방 A에서 B를 거쳐 극지방 C로 이동하는 모습을 나타낸 것이다. 지면의 위치가 변화하기 때문에 공기의 좌표계 또한 지면을 따라 회전한다. 이때 공기는 처음에 없던 z축 방향의 와도가 증가하게 되는 것이다.
모든 에너지는 보존되어야 하듯 와도 또한 보전 되어야 하기 때문에 z축의 와도가 증가하는 만큼 공기 자체의 와도는 감소하여야 한다. 따라서 상대 와도는 감소하며 시계 방향으로 회전하려는 경향이 생긴다.
이를 수식으로 나타낸다면 아래와 같다.
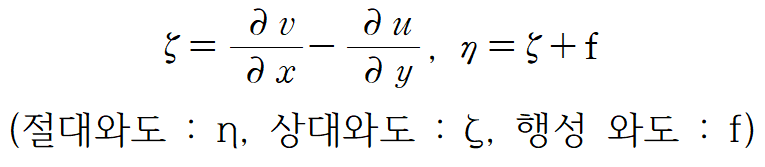
5. 맺는글
1) 와도는 회전의 경향성을 나타낸 것이며, 대기와 해양에서의 와도는 z축에 대한 와도이다.
2) 행성 와도는 지구의 자전에 의한 축의 회전이며, 상대 와도는 공기 자체의 와도이다.
3) 상대와도와 행성와도의 합을 절대와도라고 한다. 와도는 보존되어야 하므로 절대와도는 일정하다.
4) 위도가 증가하면 지표에서의 좌표계가 회전하고, 이로 인하여 z축의 와도가 증가한다.
5) 절대 와도는 일정하므로 상대와도, 즉 공기 자체의 z축 방향 와도가 감소해야 한다.
오늘은 와도에 대한 이해를 바탕으로 와도의 개념에서 부터 절대와도, 상대와도, 행성 와도에 대해 알아 보았다. 글에 대한 조회수가 많거나, 댓글이 많으면 다음에는 와위와 편서풍 파동에 대해 글을 써보려고 한다.
이해하는데 도움이 되었다면 댓글이나 공감 바란다. 한개의 공감이라도 글을 쓰는 사람에게는 큰 힘이 된다. 그럼 끝.



