천문학에서 타원 궤도 상에서 움직이는 행성, 혹은 천체를 좌표계 상에서 나타내기 위해 진근점 이각이라는 방법을 이용한다. 다만 이 글을 읽기 전 타원의 기하학적 성질, 캐플러 법칙, 원운동의 기술에 대한 기본적인 개념을 알기를 권한다.
1. 진근점 이각
진근점 이각이란, 천체의 궤도 근일점에서 부터 현재 천체가 떨어진 각거리(각도)를 뜻한다. 진근점 이각은 근일점으로 부터 반시계 방향으로 측정한다. 그런데 타원 방정식이 있는데 굳이 진근점 이각이라는 것을 정의하는 이유는 무엇일까?
아래 그럼치럼 태양을 중심으로 공전하는 목성이 있다고 가정해보자. 이때 목성의 궤도 운동에 영향을 미치는 가장 중요한 요소인 태양이 타원의 한 초점에 있기 때문에 좌표계의 축을 타원의 한 초점 위로 이동하면 여러가지 요소들을 쉽게 표현할 수 있다.
예를들어 진근점 이각, 타원의 장반경(a), 이심률(e)을 이용하여 목성의 궤도 속도를 좌표계 위에서 쉽게 표현할 수 있다.


2. 진근점 이각을 위한 타원 궤도의 요소 세가지
진근점 이각에서는 궤도의 장반경(a), 단반경(b), 이심률(e)로 모든 요소를 표현한다. 타원의 방정식을 아는 사람이라면 장반경, 단반경은 익숙하지만 이심률(e)이라는 개념은 익숙하지 않을 수 있다. 이심률이란, 각 궤도의 초점거리를 궤도 장반경으로 나누어준 값이며 궤도가 찌그러진 정도를 의미한다. 이심률은 0(완전한 원)에서 1(직선)사이의 값을 가진다.


3. 진근점 이각으로 태양-행성 거리 표현하기
이번에는 태양이 행성으로 부터 떨어진 거리(r)를 진근점 이각(θ)으로 표현해보려고 한다. 아래 그림처럼 두개의 초점 중 오른쪽의 초점에 태양이, 그리고 근일점으로부터 진근점 이각 θ인 위치에 행성이 있다고 가정해보자.
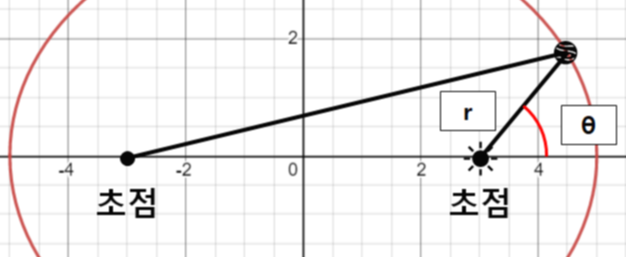
이때 아래 그림처럼 직각 삼각형을 하나 가정할 수 있다. 여기서 피타고라스 정리를 이용하면 된다.
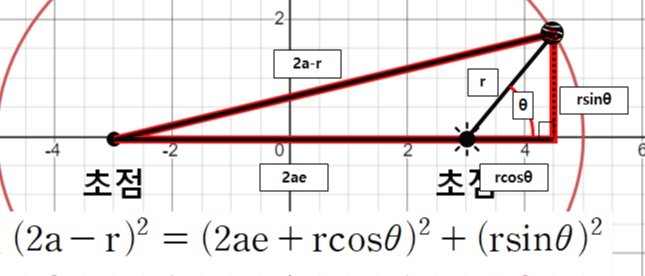
이 식을 차례대로 풀어보자.
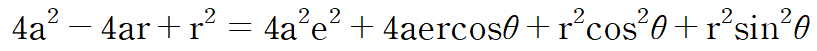
여기서 sin²θ + cos²θ = 1 이므로 양변의 r²을 제거할 수 있다. 그리고 양변에 4를 나누어주고 정리해보자.
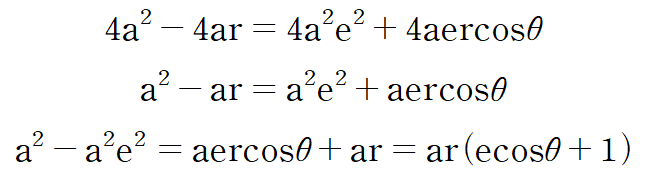
이제 이것을 r에 대해서 정리해 주면 아래와 같은 식을 얻는다.
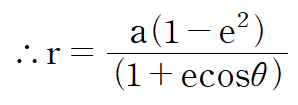
이 식을 이용하면 진근점 이각, 장반경, 이심률로 태양-행성 사이의 거리를 구할 수 있다.
4. 진근점 이각이란?
1) 행성이 근일점으로부터 떨어진 각거리를 뜻한다.
2) 진근점 이각을 쓰는 이유는 행성의 위치, 속도를 조금 더 쉽게 표현하기 위함이다.
3) 태양-행성 사이의 거리는 다음과 같이 표현할 수 있다.
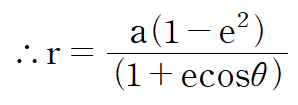
오늘은 태양계 역학을 배울 때 가장 기초가 되는 진근점 이각에 대해 알아보았다. 이 공식은 태양계 뿐만 아니라 모든 천체에 적용할 수 있다는 것을 기억하자. 다음에는 진근점 이각을 활용한 행성의 속도, 역학적 에너지를 구해보는 글을 써보도록 하겠다. 그럼 끝.



