오늘은 천체 까지의 거리를 추산하는 방법 중 운동성단에 대해 소개하려고 한다. 이 내용을 이해하기 위해서는 시선속도, 접선속도, 공간속도에 대한 개념이 반드시 필요하다. 그리고 LSR에 대한 이해가 있다면 더욱 좋다. 혹시 해당 내용을 알지 못한다면 아래 내용을 한번 참고하기를 바란다.
별의 시선속도와 접선속도, 그리고 공간속도
운동 성단에 대한 글을 쓰려다가 별의 공간 속도에 대해도 글을 써야할 것 같아서 남기는 글이다. 별의 시선속도, 접선속도, 공간속도에 대해 알아보려고 한다. 1. 별의 시선속도와 접선속도, 그
fecu.tistory.com
국부 정지 좌표계(LSR)의 이해
천문학에서 은하의 회전과 항성 운동을 배우다 보면 국부 정지 좌표계라는 것이 나온다. 은하 회전, 그리고 항성 운동은 어차피 물리학에서 모두 나오는 중력과 도플러 효과로 풀어나가기 때문
fecu.tistory.com
1. 운동성단

성단은 태양처럼 우리 은하 주변을 공전하고 있다. 성단 내에서 별들의 운동은 불규칙하지만, 전체적으로 보았을 때 별들은 한 방향으로 운동한다. 이렇게 같은 방향으로 별이 운동하는 것 처럼 보이는 성단을 운동성단이라고 한다.
운동 성단의 별들은 LSR에 대하여 모두 비슷한 방향으로 특이운동을 한다. 이때 별들의 운동을 연장하였을 때 천구상의 한 점에서 모이게 된다. 이 점을 수렴점이라고 한다.

예를들어 위와 같이 서로 평행하고, 같은 방향으로 놓여 있는 철로를 생각해보자. 철로가 서로 만나지는 않지만, 관찰자가 보았을 때는 하나의 점으로 수렴하는 것 처럼 보인다.
성단에서의 별의 운동도 마찬가지이다. 별들이 성단 내에서 제각기 다르게 운동하더라도, 별의 운동은 성단의 운동 방향으로 수렴하는 것 처럼 보인다.
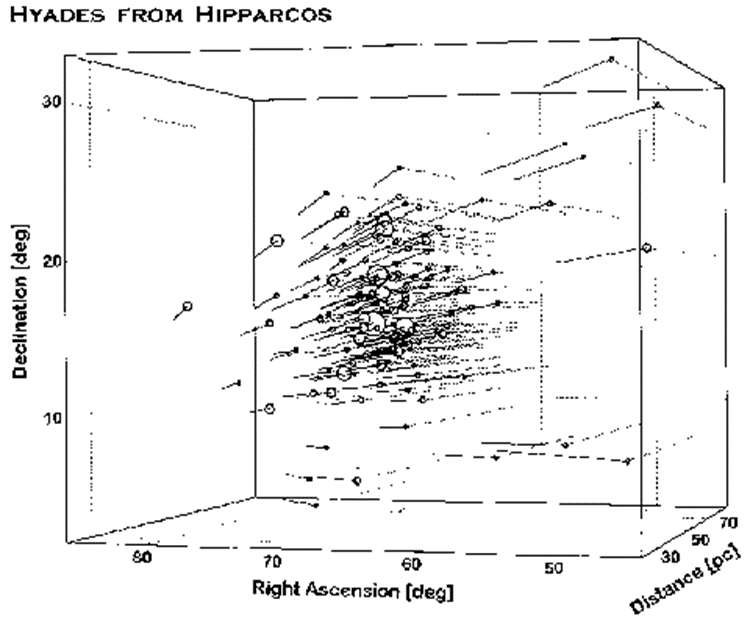
운동 성단으로 알려진 대표적인 성단은 히아데스 성단이다. 이 성단은 1900년대 초반에 운동을 모두 분석한 결과 한 수렴점에 모든 별들의 운동이 수렴한다. 그리고 성단이 가까워 천구 상에서 비교적 큰 시직경을 가지고 있기 때문에 고유운동을 통해 수렴점을 파악하기 쉽다.
2. 운동 성단을 통한 거리 측정

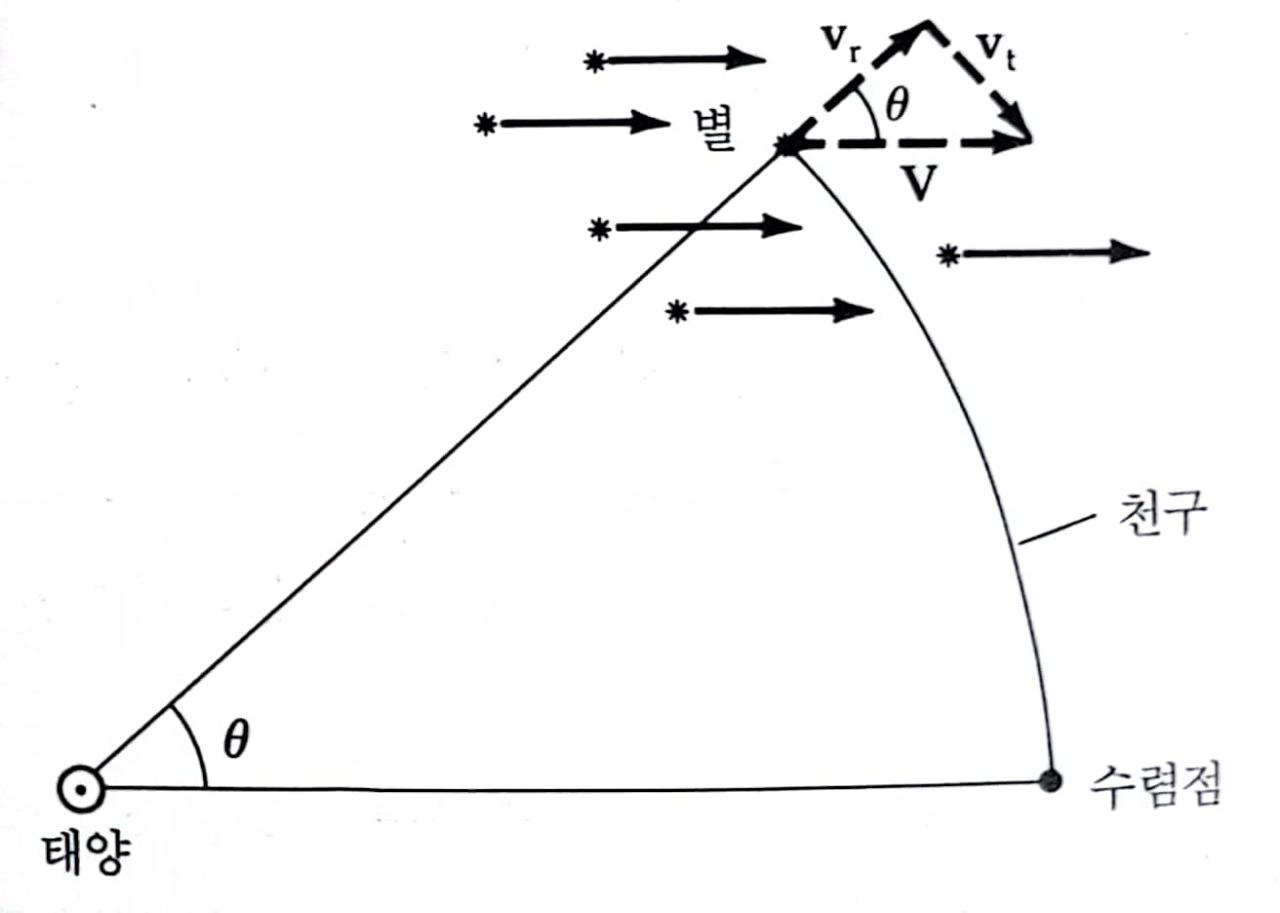
성단과 성단의 수렴점 사이의 각거리 θ는 성단의 시선 운동과 고유 운동 사이의 각도와 같다. 성단의 운동 방향을 안다면, 성단 내의 어떤 별이든 시선 속도를 구하기만 하면 성단까지의 거리를 측정할 수 있다.
별의 공간운동 속도 V와 시선속도 Vr, 접선속도 Vt는 아래와 같은 관계를 가진다.
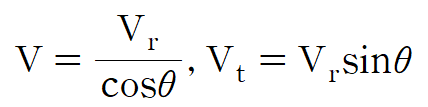
여기서 이전 포스팅에서 별의 고유운동과 시선 속도관계식을 활용하면 아래와 같은 결론을 얻을 수 있다.
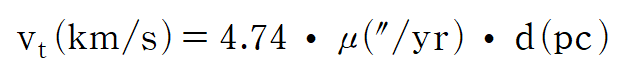
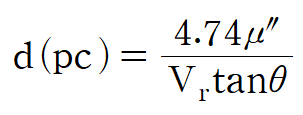
3. 결론 : 운동성단을 이용한 거리 측정
운동 성단 까지의 거리를 측정하기 위해서는 아래와 같은 조건이 필요하다.
1) 비교적 천구 상에서 큰 크기를 차지한 성단(가까운 성단)에 적용할 수 있다.
2) 성단 내에 있는 별의 고유운동, 시선속도, 수럼점을 측정할 수 있어야 한다.
3) 성단의 운동을 통해 성단 까지의 거리를 최대 500pc 이내에서 구할 수 있다.



